Building The Graph

Next up, we’ll discuss the construction of the graph abstraction that forms the underlying structure for much of the simulation. Specifically, we’ll take a look at how to transform General Transit Feed Specification into something a little more useful for simulation, including some of the (probably dangerous) assumptions that were made along the way. It’s possible some of these assumptions include some idiosyncrasies of the LA Metro data, but my hope is that is largely not the case.

The GTFS format is essentially a series of tables. The specification consists of both a required set of tables (these are generally information about physical station locations and the bare minimum information on scheduled service), and a set of optional tables that provide additional information (fares, transfers, different schedule types, etc.).

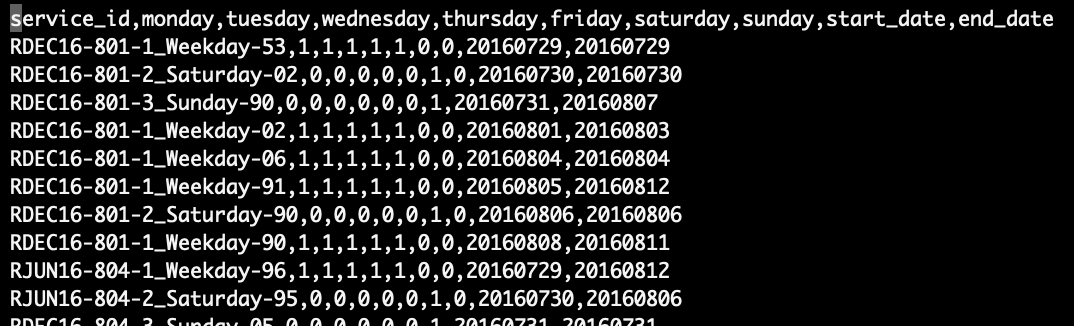Figure 1. A snippet of the calendar.txt file

There are two main pieces of information that we extract from these tables. First, we’ll extract a graph which will represent the simulated rail network, including information about which stations are adjacent and connected. Second, we’ll use the scheduling information to extract a set of routes, which we will eventually use to drive our simulations.

The Graph

Here, we will use the GTFS data to construct a directed weighted graph. We will consider all of our stations to be vertices and edges to represent the presence of a direct route between them. In order to build this from the GTFS data, we will consider all trips described in the GTFS. For each trip we consider each pair of adjacent stations: we assume they are connected and add them as a pair of vertices to our graph (if we haven’t already), where the weight is given by the time (in seconds) between the two stops. If the stations were already in the graph, we take the weight to be the minimum of the current trip time difference and any previous value. We continue in this fashion until we’ve examined all pairs of stations in all trips: at the end we have a graph representing the minimum delays between each set of stations.

In constructing the graph this way, we’ve made a couple of assumptions. First, that any two connected stations are physically adjacent. However, this might not be true, for example there may be regularly scheduled express trains which skip certain stops. We assume in such cases, that such connections still have dedicated right-of-way (think the Purple Line Express on the CTA in Chicago). While, again, this may not be true, it is suitable for our simulation.

We take the minimum value so that our graph represents the minimum distance, and therefore most closely represents the physical travel distance between stations. While this is likely very untrue, it is a necessary assumption given the nature of GTFS data, which is ultimately intended for communicating schedules, rather than complex operational data. By taking the minimum over the entire time range, we will capture the operating behaviors in the quietest time (i.e. in which trains encounter the least congestion, either from passengers, other trains, or cars on shared rights-of-way).

Figure 2. The resulting graph ignoring physical locations. Note the lines are largely disconnected, since in the LA Metro GTFS, at 7MC, Rosa Parks, and Union Station, the platforms appear as different stops.

The resulting graphs are, generally speaking, quite sparse: most transit stops are only on a single line, and even in the most well connected cities, most stops are not transfer points. Therefore our graph can be relatively efficiently represented as a list of pairs with a weight.

The Routes

Extracting the routes, is slightly more complicated. As described above, the GTFS data provides a set of trips. These trips are abstract: they represent a set of times and stations (as well as some information like the train Headsign). The calendar table then describes which trips run on each day. Therefore to find all trips that are scheduled during a time period, we loop over the days described in the calendar. For each one, we consider all the trips described as being operational that day. We then add those trips (including the set of stops and the start time of the trips) to a list of routes.

Back in the Simulator

To start with, our initial representations of the graph and routes is relatively straightforward. To actually manage the graph, we take advantage of the iGraph library, which does all the heavy lifting. We store the graph object as a sort of central oracle, which can be consulted when determining the time delay between stations.

For each run of a route, we create a new Logical Processor, which is given a list of stops and a starting time. As part of its initialization, the route LP schedules it’s first station arrival for its initial start time.

Importantly, we note that this representation is extremely wasteful: each LP simply does the work of a single scheduled trip (which is short, even in terms of simulation time), and then never does anything again. In a perfect world, we would re-use the LPs, just as real transit operations re-use the physical trains. Unfortunately, GTFS doesn’t provide sufficient information to determine which trips could be most reasonably scheduled to use the same physical train (and therefore LP). It seems likely that a simple heuristic could likely achieve reasonable re-use without too much effort, however this will have to wait until a later iteration.