The State Machine

Here, we will explore the design of the LPs that will drive the majority of the experiment. The goal here, was to model it loosely after the airplane example given in the ROSS wiki. However, despite its clarity, that example is incomplete, so I had to do a bit of just-trying-it, which may have resulted in non-optimal use of the ROSS environment. In any event, let’s get into the details.

We’ll use two types of LPs: one for the stations and another for the transit unit (trains, in this case). The idea is that once a train is started, it should progress through a predetermined route, drop off passengers, collect new passengers, and continue on its way. To achieve this, we will use a pair of complementary state machines that pass a series of messages back and forth

First, let’s take a look at the train state machine.

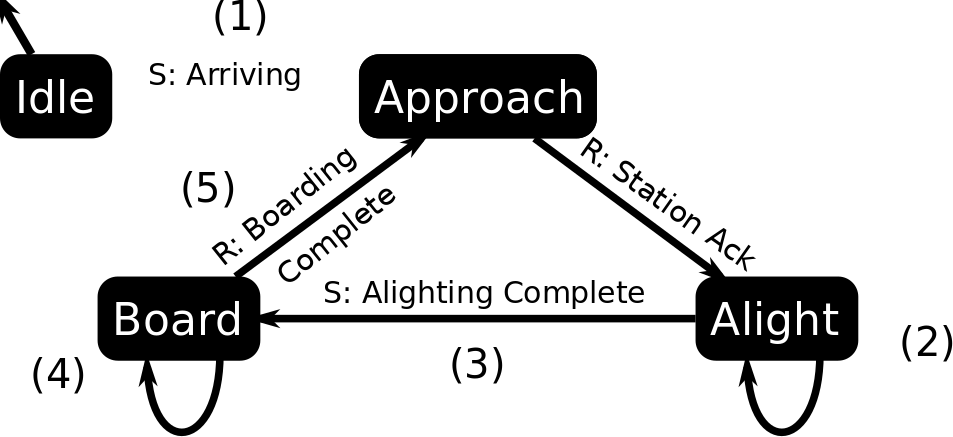
The basic flow is simple: At time (1), the train signals to a station that it’s approaching with an Arriving message. If all is clear at the station, it signals the train that it is clear to approach with a Station Ack (or its busy, in which case, it queues the train up and waits to send it a message). At (2), if the train has passengers that want to disembark, it wraps a single passenger in a message, passes it to the station. The station them acks the message. This process continues, as long as there are additional passengers to alight from the train

Once the train is out of passengers, it sends an Alighting Complete (3) message to the station, which signals boarding. At (4) opposite process then commences, with the station sending one passenger at a time. Once the station is complete, it sends a Boarding Complete message to the train at (5). The train then it computes the next station on the route, and the train begins the process anew by sending an approaching message to the next station, as in (1).

This process has few notable features, in particular as influenced by ROSS (or at least my understanding of it). First, messages (of all types) must be the same size. That means we can’t stick an arbitrary number of passengers in a single message when boarding and alighting. While there may be a clever way to solve this, my quick-and-dirty approach was to just send one at a time. While this introduces significant messaging overhead, it keeps the messages small (rather than, for example, allowing each message to hold up to N passengers).

The next interesting feature is that the messages cannot be sent instantaneously: the delay in a message must be at least the lookahead value (details of what that’s about in Parallel and Distributed Simulation Systems¹). This means all of my back and forth control signaling consumes simulation time. In order to mitigate this impact, I set the delay as low as possible (.006 in this case). The idea being this is order of magnitudes smaller than the other simulation delays from “real” causes, such as the time between stations, etc. Again, there may be a more standard ROSS way of solving this, but I sure don’t know it.

The station state machine is ultimately very similar: it waits for trains to arrive, accepts alighting passengers, waits for the alighting complete, then boards each of its passengers. Unlike the Train, the beginning of the cycle is passive the station then just waits for the next train to arrive.

So with these state machines implemented, where does that leave us? Now, with a simple hard coded route, we can have the train scoot along, even collecting and dropping-off a single hard coded passenger. I do have some concern that the above state machine will be hard to write reverse handlers for (in particular some of the loops in the boarding/alighting processes), but maybe this can be handled with some clever bit fields recording the choices, or in worst case, seq/ack numbers. But that’s a problem for the future.

1. Fujimoto, Richard M. Parallel and Distribted Simulation Systems, Wiley, 2000. ↩